Automatizing Blackbox transformation via LTL formulae
Last week, I ran two benchmarks on two RERS files, if you want to see the result, check it out here.
We can clearly see Blackbox are handling well the state space explosion problem, the number of states and transitions are drastically reduced, depending on the file.
Now we know, Blackbox is a good way to handle this problem, we want to make it easier to use, it is what I’ll be doing this week.
Combining CallGraph with variables dependencies
If we take the 2016-Problem1-ltl.go file, we can easily draw a Call Graph, so here we go :
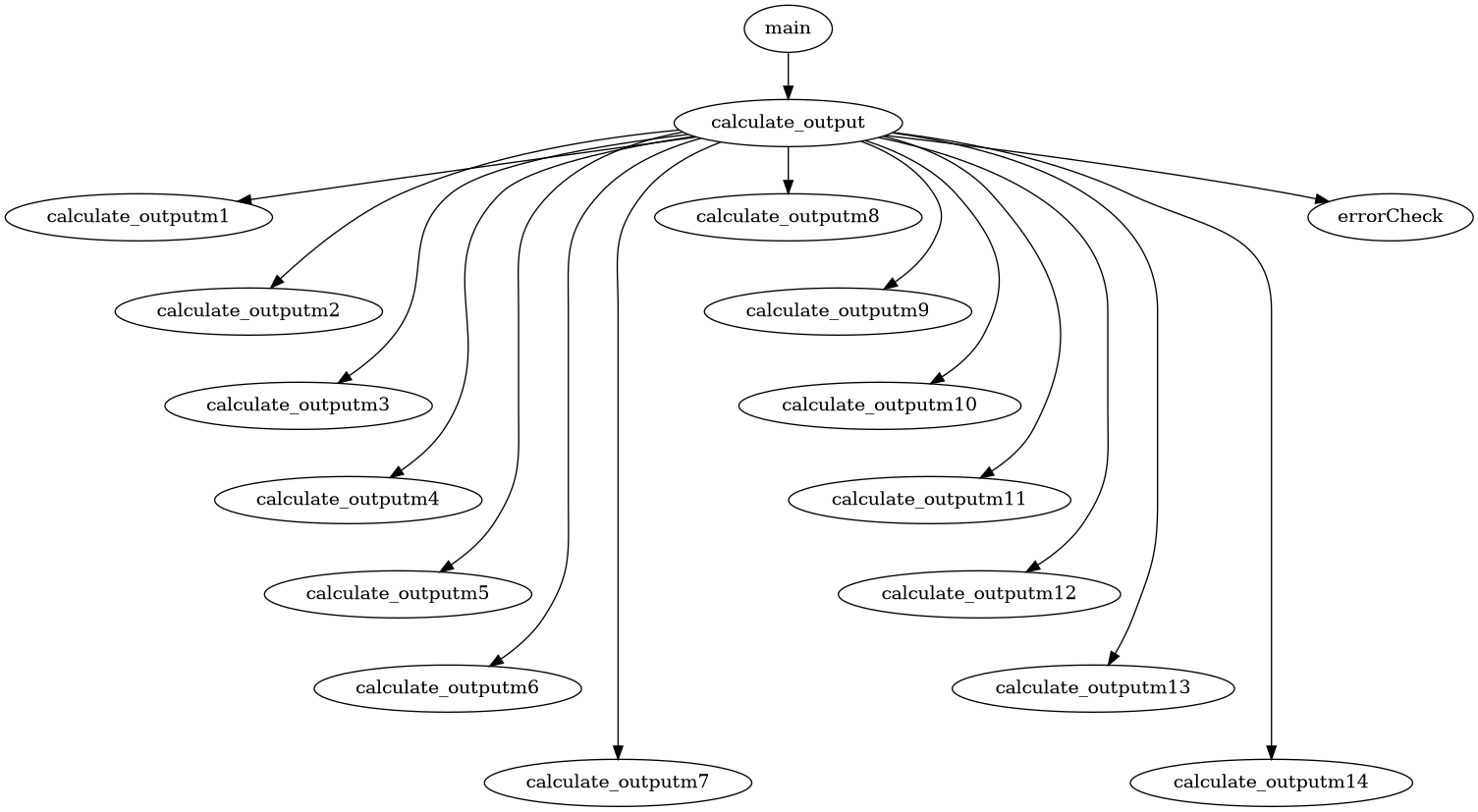 Taking our LTL formulae next, we can determinize what functions are needed.
Taking our LTL formulae next, we can determinize what functions are needed.
So let’s take one and see how it can be interpreted:
! (false R (! ("main_final_output == 19" && (true U "main_final_output == 24")) ||
((! "main_main___RERS__ == 4" ||
(! "main_final_output == 24" U (("main_final_output == 20" &&
! "main_final_output == 24") &&
X (! "main_final_output == 24" U "main_final_output == 23"))))
U "main_final_output == 24")))
We can easily parse it and obtain the wanted variables, and with it our wanted functions. In this particular case we can see the needed function is just main.
Parsing LTL formulae
So we previously saw what we need, the most basic implementation will be to browse our LTL formulae file line by line and seek for everything between quotes, once we have this, we can seek in the variables the function’s name.
Basically the idea is to maintain a map with the function’s name as key and a boolean as value, to know if this function is needed in our main thread, and not to be Blackboxed. So let’s go implement a function that does this.
A little example of what it will output with the given LTL formulae :
main true
errorCheck false
calculate_output false
calculate_outputm1 false
calculate_outputm2 false
calculate_outputm3 false
calculate_outputm4 false
calculate_outputm5 false
calculate_outputm6 false
calculate_outputm7 false
calculate_outputm8 false
calculate_outputm9 false
calculate_outputm10 false
calculate_outputm11 false
calculate_outputm12 false
calculate_outputm13 false
calculate_outputm14 false
With this we can draw again our Call Graph :
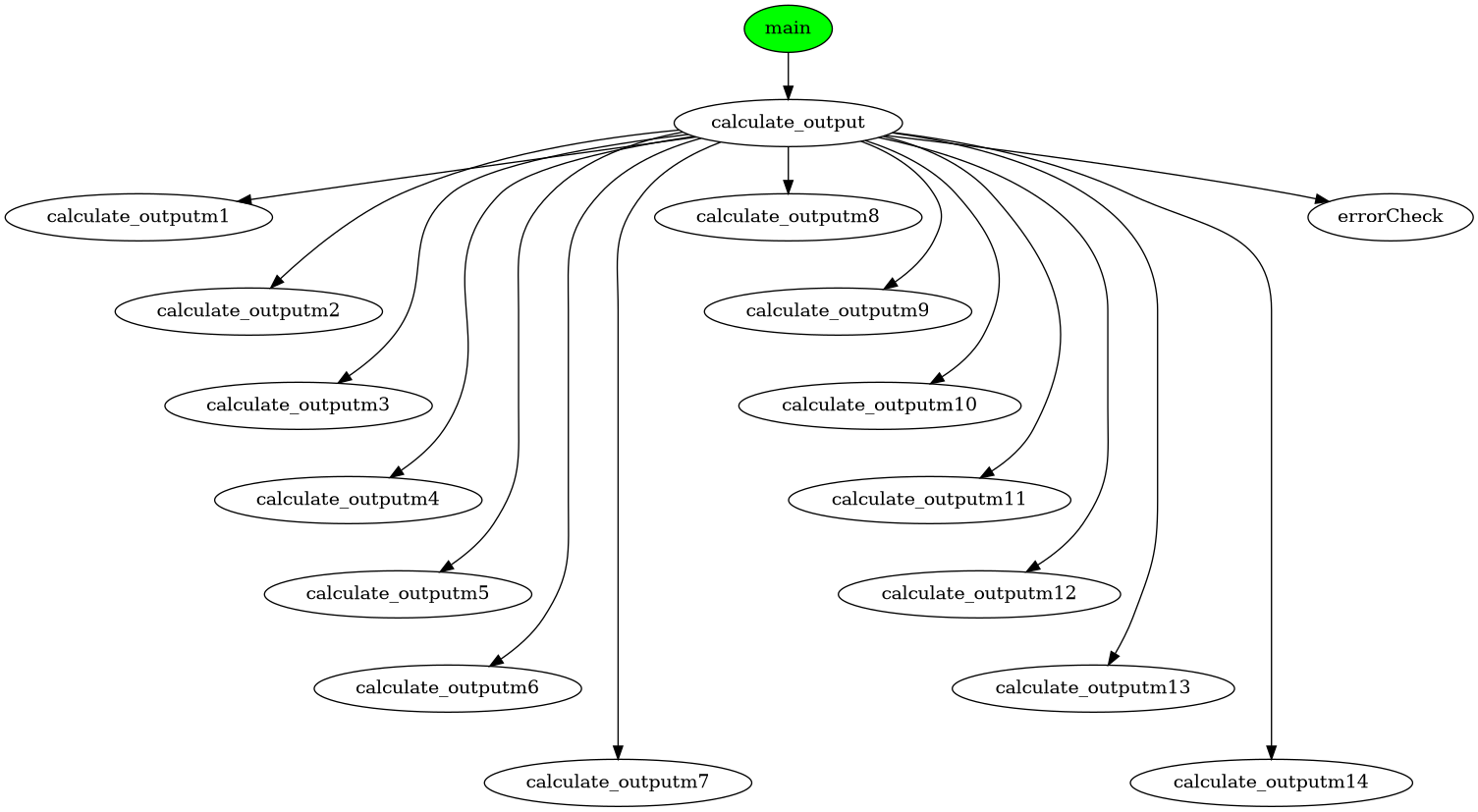 Ok it seems a little bit overkill for one function, but you need to see bigger. If we need some variables in
Ok it seems a little bit overkill for one function, but you need to see bigger. If we need some variables in calculate_outputm6 and calculate_outputm10, we will obtain something like this:
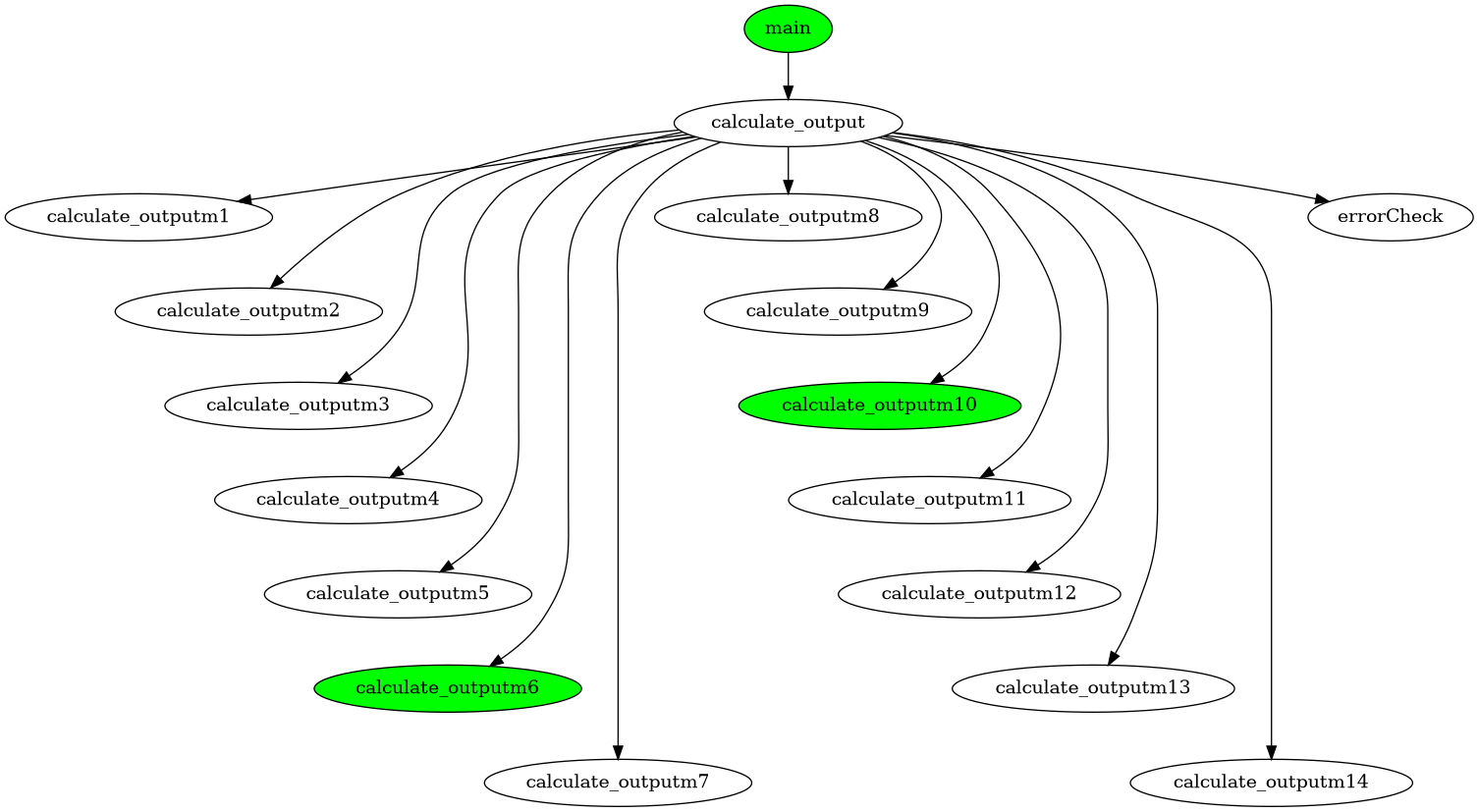
Make our Call Graph interract with our list of needed functions
We now have all the necessary elements to automatize our Blackbox transform.
For this we only need to go up in our graph from all the needed functions to the root, and mark all the function we go through as needed too.
Once again, a drawing is better than all the words in the world :
Let’s take our previous graph and apply what I just explained to you.
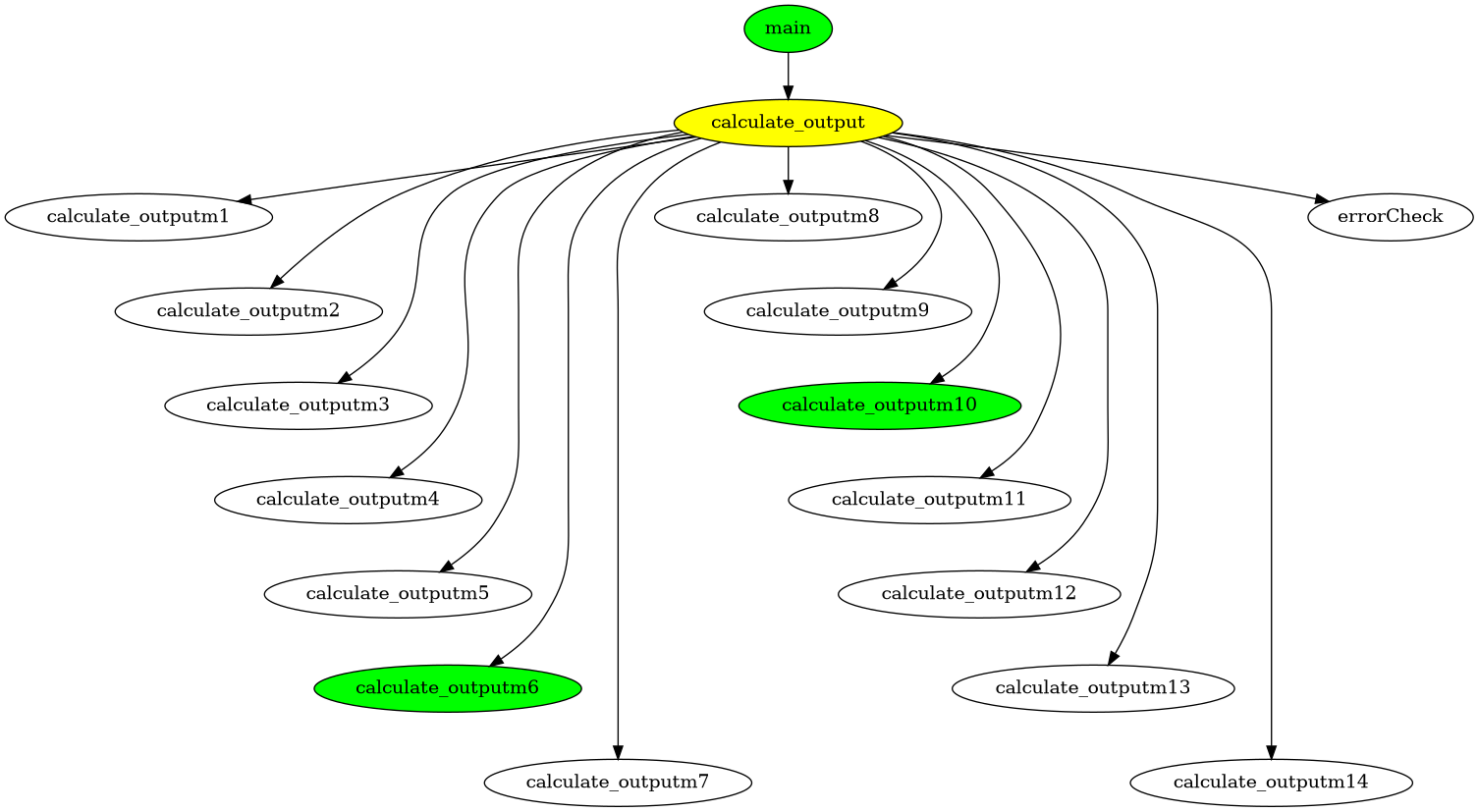 We go down in our graph, once we encounter a function that is needed, when we go up we set the caller to needed too. So
We go down in our graph, once we encounter a function that is needed, when we go up we set the caller to needed too. So calculate_output become needed too (here in yellow).
Handling more complexe cases
Let’s take a simple (but not so simple) Call Graph:
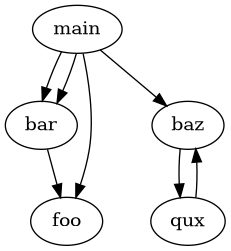 Handling Blackbox with a white list of functions seems easier, since we can decide that every caller has to be in the white list too.
If we want to have
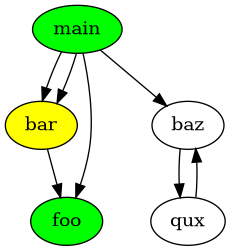
Handling Blackbox with a white list of functions seems easier, since we can decide that every caller has to be in the white list too.
If we want to have foo, we will automatically find that bar can’t be Blackbox.
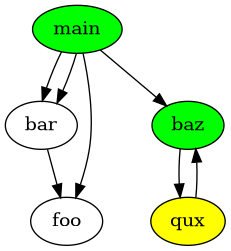
Same for baz function, since qux is a caller we can’t make it a Blackbox.
 Let’s suppose now we want to blackbox
Let’s suppose now we want to blackbox foo, there won’t be any problem, since foo isn’t calling anyone.

Let’s suppose now it is bar we want to blackbox, what should be the correct behaviour ?
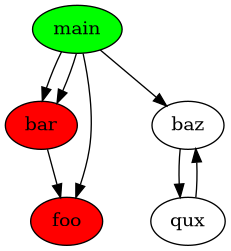
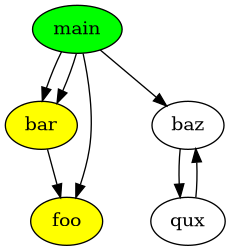
Do we decide to ignore foo because it is called by bar or do we decide to say bar can’t be Blackbox since there is a function called by it ?
So for now using a white-list rather than a black-list seems far way better, a decision should be taken deciding the correct behaviour for calling Blackbox, thus the main problem still reside in the fact that blackbox won’t be able to communicate with the main package.
Links and more
- Linear temporal logic, https://en.wikipedia.org/wiki/Linear_temporal_logic
- Clarke E.M., Klieber W., Nováček M., Zuliani P. (2012) Model Checking and the State Explosion Problem. In: Meyer B., Nordio M. (eds) Tools for Practical Software Verification. LASER 2011. Lecture Notes in Computer Science, vol 7682. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-35746-6_1
- Call Graph, https://en.wikipedia.org/wiki/Call_graph
- Golang Regexp Package, https://golang.org/pkg/regexp/